Galilei se dio cuenta de que la quinta noción común, "El todo es mayor que la parte", no era siempre correcta cuando se trataba de una infinidad de cosas. En 1638, se imprimió su libro Discorsi, en el cual explica que para cada número natural hay un cuadrado perfecto —el cuadrado de un entero como 4, 9 o 100 — y viceversa, para cada cuadrado perfecto obtenemos un número natural al sacar la raíz. Galilei concluye que hay, por consiguiente, tantos números naturales como cuadrados perfectos, no obstante que los cuadrados perfectos son sólo una parte de todos los números naturales.
Con ello, Galilei usó una noción para comparar el "tamaño" de dos conjuntos, lo que hoy se llama correspondencia uno a uno o biyección y que se introduce, por primera vez, en 1903. Galilei no persigue más esta idea y lo que encontró ha quedado simplemente como una de las paradojas del infinito. Fue Georg Cantor quien enfrentó estas paradojas de frente, al estudiar los conjuntos formalmente y, para ello, usó los números trascendentes (véase también sección 4.9). Los conjuntos no tuvieron una fácil aceptación al principio; en particular, Leopold Kronecker se oponía fervientemente.
Al principio, un conjunto era simplemente una colección de cosas. Lo único que se pedía era que, de cada "objeto", siempre se podía decidir si pertenecía o no a dicho conjunto. Relativamente pronto se dieron cuenta de que la noción, así de general, producía paradojas a su vez, como la que hoy se llama paradoja de Russell. Para este caso se considera como E el conjunto de todos los conjuntos que no se contienen como elemento y que, al usar el símbolo de pertenencia "∈", se podría escribir:
La paradoja surge entonces al preguntar si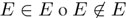 
. En el primer caso, E es un conjunto X con la propiedad 
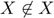, una contradicción con E ∈ E . En el segundo caso, E satisface la condición 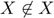y, por lo tanto, E ∈ E, lo cual es otra vez una contradicción.
Fue necesario un trabajo adicional de Ernst Zermelo y Abraham Fraenkel, matemáticos alemanes en las primeras dos décadas del siglo XX, para salvar la idea de los conjuntos y redefinirlos en forma completamente nueva. Además, Hilbert —quien era "formalista" y apreciaba la precisión y el rigor que surgió de la teoría de conjuntos a la matemática— acuñó la frase: "Nadie debe poder expulsarnos del paraíso que nos creó Cantor".
Durante la primera mitad del siglo XX tuvo lugar una gran formalización en la matemática que, además, se extendió prácticamente por toda la disciplina. Con este espíritu debe verse también la obra Principia Mathematica, de Alfred North Whitehead y Bertrand Russell. En este libro, los autores querían establecer, de una vez por todas, las bases axiomáticas para todas las matemáticas. Los autores publicaron tres tomos cubriendo "sólo" teoría de conjuntos, números cardinales, números ordinales y números reales; para ello, necesitaron aproximadamente 2 000 páginas. El cuarto tomo sobre geometría ya no lo escribieron, por agotamiento.
Hoy día, todas las matemáticas se basan —de manera formal— en la teoría de conjuntos, el sistema de axiomas ZFC, que quiere decir el sistema de axiomas de Zermelo-Fraenkel, incluyendo el axioma de elección.
